Tema 43

ESFUERZOS MECANICOS. COMPOSICI�N Y REPRESENTACI�N DE ESFUERZOS. CALCULO DE ESFUERZOS EN PIEZAS SIMPLES

1. Introducci�n a la resistencia de materiales:

����������� El estudio de los esfuerzos mec�nicos a los que est�n sometidos los s�lidos lo realiza la RESISTENCIA DE MATERIALES.

����������� Se puede definir la Resistencia de Materiales como la ciencia que estudia y desarrolla el c�lculo de la resistencia mec�nica, rigidez y estabilidad de las piezas y elementos constructivos. Entendiendo como:

* Resistencia mec�nica: la capacidad de oposici�n a la rotura.

* Rigidez: la capacidad de oposici�n a las deformaciones.

* Estabilidad: la capacidad de un elemento de oponerse a perturbaciones, manteniendo el equilibrio.

����������� Es decir, que la resistencia de materiales nos permitir� determinar el material m�s adecuado, la forma y dimensiones m�s convenientes que hay que dar a los elementos de una construcci�n o m�quina para que puedan resistir la acci�n de fuerzas exteriores que los solicitan, as� como para obtener este resultado de la forma m�s econ�mica.

����������� Estudiando la resistencia mec�nica conseguiremos dise�ar los elementos del material y medida adecuadas para evitar su rotura.

����������� Estudiando la rigidez, que se estudia cuantificando los esfuerzos interiores y las deformaciones, obtenemos las condiciones en las cuales la estructura o la pieza puede ser utilizada sin peligro de fallo.

1.1. Concepto de s�lido

����������� La resistencia de materiales tiene en cuenta tres tipos de s�lidos:

����������� a) S�lido r�gido. Es aquel que ante cualquier esfuerzo al que est� sometido, la distancia entre sus part�culas permanece invariable.

����������� Sirven para aproximar la teor�a a la realidad, simplificando enormemente los c�lculos.

����������� b) S�lido el�stico. Aquel que ante un esfuerzo exterior se deforma y recupera su forma primitiva al cesar la causa que produc�a la deformaci�n.

����������� Existen dos tipos de s�lidos el�sticos:

* S�lidos el�stico lineal.

����������� Cumplen la ley de Hooke. Las tensiones son proporcionales a las deformaciones.

Por ejemplo los aceros

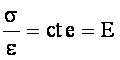
* S�lido el�stico no lineal.

����������� Las deformaciones no son proporcionales a las tensiones.

Por ejemplo las fundiciones

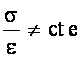
A los materiales el�sticos se les suponen dos caracter�sticas:

* La homogeneidad, tienen las mismas propiedades en todo el cuerpo.

* La isotrop�a, Las propiedades son las mismas en todas las direcciones del cuerpo.

c) S�lidos pl�sticos o elastopl�sticos. Aquellos que al someterlos a un esfuerzo, dan lugar a una gran deformaci�n y al retirar las cargas que act�an sobre el, no recuperan su forma inicial, quedando la deformaci�n permanente.

1.2. Hip�tesis de la Resistencia de Materiales

����������� En Resistencia de Materiales se debe tener siempre en cuenta el principio de la econom�a de material: Las piezas y las estructuras no deben ser superiores a las necesarias.

����������� Para ello se deben conocer bien las propiedades de los materiales y conocer una serie de hip�tesis que nos simplificaran los problemas

a) Isotrop�a y homogeneidad del cuerpo el�stico.

Isotrop�a: Las propiedades no dependen de la direcci�n elegida en su valoraci�n.

Homogeneidad: Todas las partes del mismo poseen id�ntica composici�n y caracter�sticas.

b) Continuidad.

Entre las part�culas no existen huecos, ni intersticios. La deformaci�n debida a una fuerza quede repartida de manera continua entre todos los �tomos

c) Principio de Saint Venant

El valor de las fuerzas interiores en los puntos del s�lido situados lejos de la aplicaci�n de las cargas depende muy poco del modo concreto de aplicaci�n de estas.

d) Hip�tesis de las secciones planas

Secciones planas y perpendiculares al eje de la viga antes de la deformaci�n lo contin�an siendo despu�s de la misma.

e) Principio de superposici�n de efectos

El estado final del cuerpo es independiente del orden en que se apliquen las fuerzas.

1.3. S�lido r�gido. Fuerzas exteriores e interiores

����������� En la teor�a elemental de mec�nica se considera que los cuerpos, objeto de estudi�, son r�gidos, entendi�ndose cuerpos r�gidos como aquellos que no se deforman bajo la acci�n de fuerzas aplicadas sobre dichos cuerpos. En realidad no son absolutamente r�gidos y se deforman bajo la acci�n de las fuerzas a las que son sometidos, siendo las deformaciones normalmente peque�as y no afectan apreciablemente a las condiciones de equilibrio. Sin embargo, son importantes estas deformaciones en la resistencia a la� rotura de las estructuras y son estudiadas en la resistencia de materiales.

����������� Igual que en un sistema de part�culas, un s�lido r�gido puede estar sometido a fuerzas exteriores y fuerzas interiores.

Las fuerzas exteriores son debidas a la acci�n de otros cuerpos sobre el s�lido r�gido considerado, siendo responsables del comportamiento externo del s�lido r�gido, es decir, provocar�n el movimiento del s�lido o har�n que permanezca en equilibrio.

Las fuerzas interiores tienen como misi�n mantener unidas entre s� todas las part�culas de las que est� formado el s�lido r�gido, y si nuestro s�lido r�gido est� compuesto estructuralmente por varias partes, las fuerzas que mantienen la uni�n se definen tambi�n como fuerzas interiores.

1.4. Condiciones generales de equilibrio en un s�lido r�gido

Todo sistema de fuerzas puede sustituirse por una fuerza (resultante) y un par de fuerzas (momento resultante).

����������� Como consecuencia de lo anterior, se puede expresar como condici�n necesaria y suficiente para que un s�lido r�gido est� en equilibrio, que la resultante y el momento resultante respecto a un punto cualquiera del s�lido de las fuerzas exteriores que act�an sobre el sean iguales a cero.

Es decir:��

����������� Cuando nos encontremos ante un caso pr�ctico y debamos establecer las condiciones de equilibrio, el primer paso ser� establecer el sistema de fuerzas exteriores que act�a sobre el s�lido r�gido, diagrama de cuerpo libre, donde entenderemos por fuerzas exteriores, no solo las cargas a las que est� sometido el cuerpo y la acci�n de la gravedad, sino tambi�n las fuerzas de reacci�n ejercidas sobre el s�lido por las superficies de apoyo, los pasadores, soporte de rodillo, etc.

����������� Una vez determinadas todas y cada una de estas fuerzas, y elegido nuestro sistemas de ejes rectangulares, bastar� con especificar el sistema de ecuaciones correspondientes para imponer el equilibrio en s�lido r�gido.

1.5. Cargas. Fuerzas externas.

����������� Si se a�sla un elemento resistente de los cuerpos a los que esta ligado, las acciones que estos ejercen sobre �l, se ven sustituidas por fuerzas , a las que llamamos exteriores.

����������� Hay dos tipos de solicitaciones exteriores:

����������������������� Fuerzas activas � denominadas cargas.

����������������������� Fuerzas de reacci�n � denominadas reacciones.

����������� Tanto las cargas como las reacciones est�n formadas en general por un fuerza y un momento.

����������� Clasificaci�n de las cargas

* De volumen:

����������� Son las debidas a los campos de fuerza (gravitatorias). Peso propio.

* De superficie.

����������� Son las que se aplican en la superficie del s�lido.

Concentradas: Son cargas puntuales.

Distribuidas: Son cargas por unidad de superficie. Por ejemplo la acci�n del viento.

* Seg�n el tiempo que dure su aplicaci�n.

Permanentes o concarga:

Mantienen su posici�n y magnitud a lo largo del tiempo. Se descomponen en dos:

Peso propio: carga debida al peso propio del elemento resistente

Carga permanente: debido al peso de los elementos constructivos

Sobrecargas o accidentales:

Son cargas cuya magnitud y posici�n puede ser variable a lo largo del tiempo.

Son : De uso y explotaci�n.

Sobrecarga de nieve.

Sobrecarga de viento.

* Atendiendo a su variaci�n en el tiempo.

Est�ticas: su magnitud y/o punto de aplicaci�n var�a muy lentamente. (Se puede prescindir de las fuerzas de inercia).

Din�micas: var�an con el tiempo. La acci�n de estas fuerzas crea vibraciones apareciendo fuerzas que pueden superar a las fuerzas est�ticas.

De repetici�n peri�dica � C�clicas � fatiga

De repetici�n no peri�dica � Choques

1.6. Reacciones y tipos de apoyos

����������� Se define ligadura, como todo dispositivo que impide de un modo total o parcial, el libre movimiento de un s�lido.

����������� La ligadura es un v�nculo de uni�n con el resto de los elementos que componen una estructura.

����������� Un elemento resistente tiene seis grados de libertad cuando est� libre, es decir puede desplazarse y girar sobre y alrededor de los tres ejes de coordenadas.

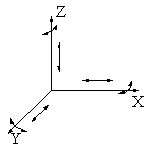
Tipos de ligadura y de apoyos:

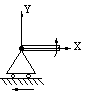
� Apoyo articulado m�vil:

S�lo existe una reacci�n perpendicular al plano de apoyo � una sola reacci�n de ligadura.

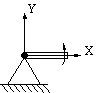
� Apoyo articulado fijo:

El desplazamiento est� impedido en todas las direcciones � Existen dos reacciones en los ejes X e Y

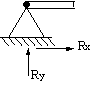
� Apoyo empotrado o empotramiento

En el est�n impedidos los desplazamientos en el plano OXY y los giros. Existen tres reacciones de ligadura

2. Estudio de los estados solicitantes de un prisma mec�nico

����������� Partimos de un prisma mec�nico que supondremos en equilibrio y que soporta un sistema de fuerzas F_i (i=1...n), que representa a las cargas exteriores al mismo aplicadas. Se consideran los ejes en el centro de gravedad del prisma mec�nico.

����������� Para analizar las reacciones internas, cortamos el prisma por una secci�n de estudio y lo aislamos.

����������� Para mantener el equilibrio en la parte que permanece, la zona del prisma suprimida genera un torsor equivalente a la acci�n externa ejercida sobre la parte eliminada. (Mantiene al s�lido en equilibrio).

������������������ ���������������

Torsor ()

����������� Las fuerzas a los que se ve sometido el prisma� son:

a) Fuerzo normal V_x� (da lugar a la tensi�n normal s_n)

Se nombra con la letra N. Tiende a separar o a unir ambas partes del s�lido, originando tracciones y compresiones.

b) Esfuerzos cortantes V_y,V_z (dando lugar a las tensiones de cortadura t)

Tratan de cortar la secci�n (deslizar una parte respecto de la otra)

����������� Los momentos generados son:

a) Momento torsor

Se nombra como M_T. Tiende a hacer rotar el cuerpo respecto del eje x.

b) Momentos flectores

Provocan rotaciones laterales, ocasionando la flexi�n del cuerpo

3 Tracci�n y compresi�n

3.1 Esfuerzos y deformaciones

����������� Entre los �tomos de los cuerpos s�lidos existe un sistema de fuerzas internas en equilibrio , a diferencia de lo que ocurre en l�quidos y gases.

����������� Todos los cuerpos s�lidos, debido a estas fuerzas, se resisten a ser deformados cuando son sometidos a fuerzas externas (cargas). Presentan por tanto una resistencia a la deformaci�n.

����������� En Resistencia de Materiales se entienden los esfuerzos como fuerzas imaginarias que aparecen en el interior de los elementos o piezas cuando est�n sometidos a cargas exteriores. Estos esfuerzos modelizan el comportamiento real de los elementos. Se denominan deformaciones a las variaciones de sus dimensiones iniciales por efecto de las fuerzas aplicadas.

����������� Supongamos que tenemos una barra de acero y longitud inicial l₀ y aplicamos a sus extremos dos fuerzas iguales y opuestas, P, alineadas con el eje de simetr�a del material las cuales tienden a estirar el material. Se dice entonces que la barra est� sometida a tracci�n. Debido a estas fuerzas la barra se deforma, es decir, sufre un alargamiento, d. La longitud final ser� por tanto

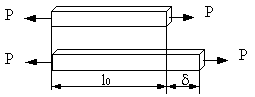
����������� Se denomina deformaci�n unitaria, e, a la deformaci�n de la barra por unidad de longitud. Su valor vendr� dado por el cociente entre el alargamiento d y la longitud inicial l_0.

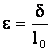�(adimensional)

����������� Dos caras contiguas de una secci�n recta cualquiera permanecen unidas en una pieza sometida a tracci�n, por que aparece una fuerza interna, uniformemente distribuidas sobre toda la secci�n.

����������� Esta distribuci�n uniforme de fuerzas es lo que se denomina esfuerzo. Tambi�n llamado tensi�n. El valor de su intensidad, s, viene establecido por el cociente entre la carga exterior aplicada , P, y el �rea de la secci�n recta inicial sobre la que act�a A₀

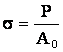
Las unidades ser�n N/mm² . Aunque la m�s com�nmente utilizada es Kg/cm²

* Principio de St. Vennant

����������� La formula anterior la podemos aplicar en materiales homog�neos e is�tropos, es decir en materiales que tienen la misma composici�n en cada punto.

����������� En la cercan�a del punto donde se ha aplicado la fuerza exterior se producen efectos locales, que nos dan como resultado una distribuci�n no uniforme de las tensiones, lo mismo que ocurre en las proximidades de los cambios de secci�n, debido a que son zonas de acumulaci�n de esfuerzos.

Sin embargo podemos establecer que para puntos suficientemente alejados de estas zonas la formula nos aproxima con suficiente fiabilidad a la realidad. Para elementos delgados, a una distancia tres veces la anchura de la barra pueden suponerse despreciables esos efectos locales. Est� hip�tesis se conoce con el nombre de Principio de St. Vennant

3.2 Resistencia a la tracci�n. Elasticidad-Plasticidad

����������� La elasticidad es una de las propiedades mec�nicas de los materiales. Est� relacionada con la deformaci�n que sufren cuando se les somete a cargas exteriores. Se puede definir como la cualidad que tienen los cuerpos de recuperar su forma primitiva cuando se les descarga de las fuerzas aplicadas. Si el elemento deformado recupera totalmente sus dimensiones iniciales cuando se eliminan las cargas exteriores aplicadas se dice que ha sufrido una deformaci�n el�stica. Por el contrario, si al eliminar las cargas exteriores el elemento queda con deformaci�n permanente se dice que ha experimentado una deformaci�n pl�stica.

����������� El m�todo mas usual para determinar est� y otras propiedades mec�nicas en los metales es el Ensayo de tracci�n. Este ensayo relaciona la deformaci�n que va sufriendo la probeta se metal con la carga creciente que se le va aplicando. De �l obtenemos el diagrama tracci�n deformaci�n, que representa el esfuerzo que sufre la barra, referido a su secci�n inicial, en funci�n de la deformaci�n unitaria, respecto a su longitud primitiva, obtenemos una curva como la de la figura.

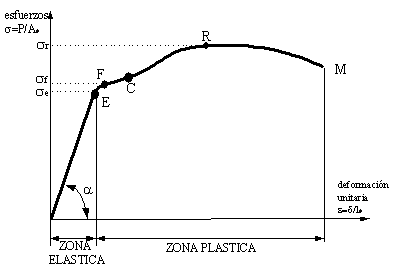
����������� Hasta llegar al punto E, llamado limite el�stico, la deformaci�n es proporcional a la carga, es decir, entre los esfuerzos y las deformaciones unitarias se establece una relaci�n lineal. En esta zona el material trabaja de forma el�stica y se dice que responde a la ley de Hooke, (enunciada en 1678). �Las deformaciones son proporcionales a las fuerzas deformadoras�.

����������� El esfuerzo correspondiente al punto E, s_e, se denomina l�mite de elasticidad del material y se puede definir, como el mayor valor esfuerzo del esfuerzo que origina deformaciones el�sticas. Con esfuerzos mayores que este el material sufre ya deformaciones pl�sticas, es decir, queda con deformaci�n permanente.

����������� La constante de proporcionalidad entre esfuerzos y deformaciones unitaria en esta zona lineal se denomina Modulo de Elasticidad o Modulo de Young

s=E e

El Modulo de Elasticidad es una caracter�stica de cada material y depende s�lo de su estructura interna, normalmente puede considerarse constante.

����������� Con cargas superiores al limite el�stico, punto E, la relaci�n entre cargas y deformaciones ya no es lineal. El diagrama se curva hasta llegar al punto F, llamado punto de fluencia, siendo s_f el esfuerzo de fluencia correspondiente. En esta situaci�n la barra se alarga sin apenas incremento de carga, tramo FC. Si en el punto C desapareciese al carga, el material recuperar�a el�sticamente parte de su longitud quedando una deformaci�n permanente.,

����������� A partir del punto C es necesario aumentar la carga para producir nuevas deformaciones.

����������� A partir del punto de fluencia si incrementamos m�s la fuerza aplicada, la deformaci�n es muy r�pida con poco incremento de la carga. El esfuerzo va aumentando hasta llegar el punto R, carga m�xima, a partir del cual prosigue la deformaci�n hasta la rotura, punto M son que la carga aumente. Aunque el material f�sicamente rompe en el punto M , se dice, que la carga del punto R es la carga de rotura, siendo s_r el esfuerzo de rotura correspondiente.

����������� Los esfuerzos correspondiente al limite de elasticidad, se al punto de fluencia s_f y a la carga de rotura s_r definen las caracter�sticas resistentes de los materiales.

����������� Se han de dimensionar siempre los elementos de estructuras y m�quinas para que trabajen siempre en condiciones el�stica, es decir, dentro de la recta OE

4 Cortadura

4.1 Esfuerzo normal y esfuerzo cortante en la tracci�n

����������� Una fuerza de tracci�n origina en una secci�n recta del material un esfuerzo que viene dado por la ecuaci�n

����������� En una secci�n inclinada cualquiera, cuya normal forma un �ngulo f el eje de la barra, la fuerza de tracci�n tambi�n generada un esfuerzo , que podemos considera uniforme en toda la secci�n, que ser� menor que el producido en la secci�n recta, al ser menor el �rea

�

����������� La relaci�n entre la �reas es la siguiente

��

Si f = 0�� s_mn=s_x, o sea los esfuerzos m�ximos ocurren en la secciones normales.

Si f= 90�� s_mn=0 o sea en las secciones paralelas a la carga no hay esfuerzos.

����������� En un punto cualquiera de la secci�n inclinada podremos descomponer la tensi�n dada s_nn en dos componentes, normal y paralela a la secci�n. Obteniendo los valoress_n1, esfuerzo normal y t₁ esfuerzo cortante.

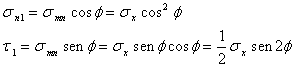
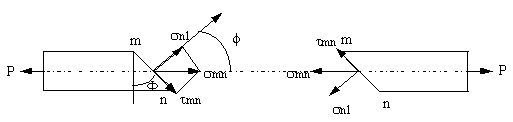
����������� Los esfuerzos en una secci�n cualquiera de una barra sometida a tracci�n son de dos tipos: esfuerzos normales s_n1, perpendiculares a la secci�n y que intentan arrancar los dos trozos en que dicha secci�n divida la barra, Y esfuerzos cortantes t₁, paralelos a la secci�n, los cuales fuerzan el deslizamiento de una cara de la secci�n sobre la otra cara.

4.2 Esfuerzo normal y cortante en la compresi�n

s_n

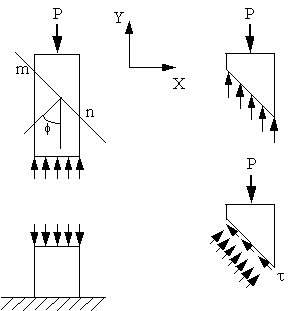
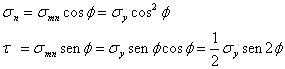
4.3 Teor�a elemental de la cortadura

����������� Una secci�n recta del prisma mec�nico, decimos que est� sometida a cortadura pura cuando, en dicha secci�n, act�an �nicamente tensiones tangenciales que se reducen a una resultante contenida en el plano la misma, fuerza cortante.

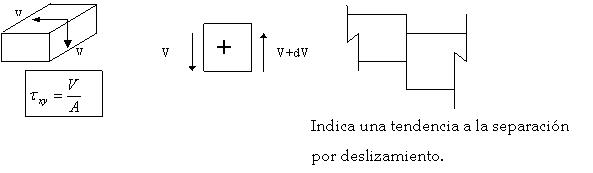
����������� Cuando en una secci�n recta de un prisma mec�nico la resultante de las fuerzas situadas a un lado de la misma est� contenida en su plano y el momento resultante es nulo, diremos que esa secci�n del prisma trabaja a cortadura pura. Pero si esto ocurre en una determinada secci�n, en las secciones pr�ximas existe tambi�n un momento flector M producido por esta resultante, es decir, no es posible que en un tramo finito de un prisma mec�nico se d� en todo �l un estado de cortadura pura.

����������� En el c�lculo de elementos de uni�n, como tornillos, remaches o cordones de soldadura, se suele admitir la presencia �nicamente del esfuerzo cortante y la nulidad del momento flector en todas las secciones. Esto es aceptable porque, en estos elementos, los efectos (las tensiones y deformaciones) debidas al esfuerzo cortante son mucho mayores que los debidos al momento flector.

����������� Las cargas verticales est�n contenidas en este plano, adoptaremos para el esfuerzo cortante t el convenio de signos indicado en la figura. La tendencia a la rotura de la barra para t positivo se indica asimismo en la misma.

����������� En la teor�a elemental se admiten las siguientes hip�tesis:

1. Hip�tesis de Bernoulli, seg�n la cual las secciones rectas permanecen planas despu�s de la deformaci�n.

2. La tensi�n tangencial t que produce el esfuerzo cortante tiene la misma direcci�n que �ste.

����������� Un ejemplo t�pico del c�lculo por deslizamiento, lo constituye el c�lculo de juntas remachadas, soldadas o a base de pernos.

4.4 Calculo de elementos a cortadura

�������� Uniones roblonadas y atornilladas

����������� Existen algunas estructuras o piezas de determinadas m�quinas que est�n compuestas de elementos que hay que unir de forma adecuada para que cumplan la funci�n para la que han sido dise�adas. Si se trata de materiales met�licos, los medios de uni�n com�nmente empleados son remaches, tornillos y soldadura. Las uniones con bulones tienen poca aplicaci�n, y las uniones por medios adhesivos se encuentran a�n en fase experimental.

����������� La distribuci�n de tensiones en estos medios de uni�n es bastante compleja, dependiendo en gran parte de las deformaciones propias de los elementos que la constituyen. Esto hace que el c�lculo riguroso de las uniones sea siempre dif�cil y muchas veces imposible de realizar. Por esto. en el terreno pr�ctico es necesario contrastar los resultados obtenidos aplicando los m�todos simplificados de c�lculo, con el comportamiento real de los materiales de en las uniones.

����������� Las uniones roblonadas se llevan a cabo mediante piezas denominadas roblones o remaches. Un robl�n es un elemento de uni�n que est� formado por una espiga cil�ndrica llamada ca�a, uno de cuyos extremos tiene una cabeza esf�rica, bombeada o plana, llamada cabeza de asiento. El robl�n se introduce, calent�ndolo previamente entre 1050 �C (rojo naranja) y 950�C (rojo cereza claro), en un agujero efectuado en las piezas a unir y se golpea bien con martillo neum�tico o m�quina roblonadora de presi�n uniforme en el otro extremo, para formar una segunda cabeza (cabeza de cierre) que asegure la uni�n. Cuando se efect�a en fr�o esta uni�n se llama remachado, aunque lo m�s normal es que se use ese nombre siempre.

����������� El robl�n al, enfriar, se contrae originando en el esfuerzos de tracci�n que son los que originan la presi�n entre la piezas a unir. Este rozamiento entre ellas es el que soporta la fuerza de cizallamiento o cortadura. Aunque suceda esto, el c�lculo se realiza suponiendo que no hay tracci�n sobre el robl�n, y que este el� que aguanta toda la cortadura

����������� Las uniones remachadas y atornilladas se dice que trabajan a cortadura cuando las fuerzas se transmiten por contacto entre las chapas a unir y la ca�a de los remaches o tornillos. Cuando la transmisi�n se realiza por contacto entre la chapa y la cabeza del elemento de uni�n �ste trabaja a tracci�n. El caso m�s normal es el de uniones trabajando a cortadura, y es �ste el que vamos a estudiar a continuaci�n.

����������� Distinguiremos dos tipos de uniones remachadas o atornilladas seg�n las cargas aplicadas est�n centradas respecto al elemento de uni�n o se trate de cargas exc�ntricas respecto a �stos.

����������� Dentro de los del primer grupo distinguiremos a su vez si los remaches o tornillos trabajan a cortadura simple (por una secci�n) o a cortadura doble (por dos secciones).

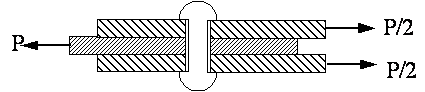
����������� Las posibles causas de fallo de una uni�n remachada o atornillada trabajando a cortadura son las siguientes:

a) Fallo por cortadura.

����������� Si la tensi�n de cortadura en los remaches o tornillos es superior a la tensi�n admisible s_adm del material de los remaches, la uni�n se romper�a por la secci�n del remache sometida a cortadura. Se puede aumentar la resistencia de la uni�n aumentando el di�metro de los remaches o poniendo mayor n�mero de ellos.

����������� En la secci�n entre planchas el robl�n trabaja a cortadura, siendo el valor de t:

Siendo d el di�metro del robl�n

����������� En el caso de elementos que trabajan a doble cortadura, es decir en aquellos casos en los que se presenten dos o mas planos de corte el valor de la tensi�n tangencial ser�:

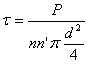
Siendo n el n�mero de roblones y n� el n�mero de planos de corte

b) Fallo por aplastamiento.

����������� La uni�n podr�a fallar si un remache aplastara el material de la placa en la zona de contacto com�n, o bien, si el propio remache fuera aplastado por la acci�n de la placa. Como la distribuci�n de tensiones en la zona de contacto es sumamente compleja, a efectos pr�cticos de c�lculo se considera que el esfuerzo de aplastamiento se reparte uniformemente en el �rea proyectada de la espiga del remache sobre la placa, es decir, sobre el �rea d x e. Se puede aumentar la resistencia a compresi�n de la uni�n aumentando el �rea de compresi�n, o sea, aumentando el di�metro del remache o el espesor de la placa, o ambos.

����������� Para determinar la tensi�n debida al aplastamiento producida por la acci�n compresiva del robl�n sobre la plancha, se supone que la presi�n se realiza de manera uniforme sobre la zona de contacto entre chapa y robl�n. Se toma como �rea de contacto

A_contacto = d*e

Siendo d el di�metro del robl�n y e el espesor m�nimo de la plancha

La tensi�n de aplastamiento valdr�:

c) Fallo por rotura de la placa o tracci�n.

����������� En una pieza sometida a tracci�n, de una uni�n mediante remaches, se puede producir el fallo por rotura de la secci�n debilitada por los agujeros para los remaches. A efectos pr�cticos del c�lculo se admite la hip�tesis de ser uniforme la distribuci�n de tensiones en la secci�n neta de la placa, esto es, descontando al �rea de la secci�n recta de la placa la correspondiente a los agujeros de los remaches o tornillos. Se puede elevar la resistencia de la uni�n aumentando el espesor o el ancho de la placa, o ambos.

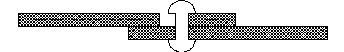
����������� La secci�n m�nima de trabajo se dar� en donde est�n situados los roblones, pues ah� la secci�n primitiva de la plancha se ve reducida, siendo el valor de la secci�n �til:

A_�til= ( c-n��d) e

Siendo la tensi�n de tracci�n en la plancha:

����������� Puede evitarse la rotura de la plancha, debida a la colocaci�n de roblones excesivamente pr�ximos al borde, manteniendo una distancia aproximadamente de tres veces el di�metro del agujero, este margen se conoce como solape.

d) Fallo por cortadura de la placa.

����������� Se produce este fallo por desgarro de la placa en la parte situada detr�s del remache. Este fallo se evita aumentando la superficie de la placa sometida a cortadura, es decir, dando suficiente longitud a la placa detr�s del remache, como puede ser el de dos a tres veces el di�metro del remache.

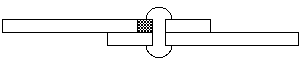
����������� Las roturas por fallo de la chapa a tracci�n o cortante no se suelen considerar en el c�lculo de la uni�n, ya que se evitan al tener en cuenta las recomendaciones de las normas en cuanto a distancias m�nimas entre agujeros, y entre �stos y los bordes de las chapas. No obstante, la comprobaci�n de una determinada uni�n a estos dos posibles fallos no reviste ninguna dificultad. Se utilizar� la tensi�n admisible a tracci�n en el primer caso y la tensi�n admisible a cortadura en el segundo, tensiones en ambos casos referentes al material de la pieza que puede presentar esos fallos.

5 Flexi�n

����������� Un elemento estar� sometido o trabajando a flexi�n cuando est� aplicada una fuerza exterior o� carga sobre �l de tal manera que produzca una deformaci�n del eje en forma longitudinal.

����������� El c�lculo de los esfuerzos se va a realizar sobre elementos gen�ricos utilizados en mec�nica, los elementos viga.

����������� Se considera que las vigas son prism�ticas y con un plano longitudinal de simetr�a. Las cargas est�n aplicadas en ese plano.

Para el c�lculo de los esfuerzos y deformaciones en la vigas est�s han de estar en equilibrio est�tico, es decir, las fuerzas o los momentos directamente aplicados, junto con las fuerzas o momentos de reacci�n en los apoyos han de conformas un sistema en equilibrio.

����������� Para los determinaci�n de las reacciones en los apoyos de las vigas usaremos las ecuaciones de la Est�tica que rigen el equilibrio en el plano, a saber:

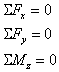
����������� Si aplicando las ecuaciones anteriores podemos determinar el valor de todas las reacciones en los apoyos se dice que la viga es est�ticamente determinada. En cambio si hay m�s reacciones que ecuaciones el sistema es indeterminado o hiperest�tico, necesitando m�s ecuaciones para resolverlo.

5.8 Determinaci�n de Momentos Flectores.

����������� El dimensionado de la viga exige el conocimiento de los valores que adopta el momento flector en cada secci�n de la misma.

����������� Como norma general a la hora de estudiar una viga se seguir�n los siguientes pasos:

����������� 1.- Determinaci�n del car�cter de la viga: Isost�tica o hipererest�tica.

����������� 2.- C�lculo de las reacciones sobre los apoyos:

* Aplicando las ecuaciones de la est�tica (SF=0, SM=0), en caso Isost�tico.

* Aplicando las ecuaciones de la est�tica y alguna condici�n de contorno, en el caso hiperest�tico.

����������� 3.- Determinaci�n de los diagramas de momentos flectores y esfuerzo ���� ������cortantes.

����������� 4.- Determinaci�n de las secci�n mas peligrosa y c�lculo de la secci�n ���� �����total de la viga con los datos obtenidos en la secci�n m�s peligrosa.

����������� El c�lculo de las reacciones en los apoyos y la determinaci�n de del diagrama de momentos flectores depende del tipo de apoyos y de la distribuci�n de la carga sobre la viga.

����������� Como ejemplo se estudiar� el caso de vigas isost�ticas simplemente apoyadas, con tres tipos de cargas: Carga puntual, carga uniformemente distribuida y carga con una distribuci�n triangular

����������� a) Viga simplemente apoyada con una carga puntual aplicada en el centro de la viga.

����������� En primer lugar determinaremos las reacciones:

S F_V = 0�

Tomando momentos respecto del punto medio:

S M_O=0 �

Despejando en las dos ecuaciones obtenemos R_A=R_B=P/2

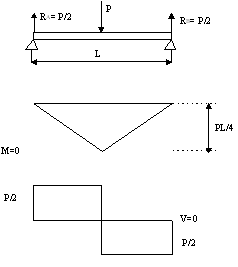
Leyes de momentos flectores

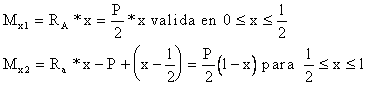
����������� El momento flector m�ximo se presentar� en el punto medio de la viga, su valor ser�:

����������� b) Viga simplemente apoyada con una carga uniformemente distribuida

-

����������� Se representa por P la carga por unidad de longitud. Suele expresarse en toneladas por metro lineal (ton/m).

����������� Las reacciones se determinan por simetr�a:

����������� En este caso s�lo existe una ecuaci�n de momentos para toda la viga:

ecuaci�n de una par�bola, por lo que el diagrama de momentos flectores ser� un arco de este tipo de c�nica.

����������� Para hallar el momento flector m�ximo se iguala a cero la primera derivada:

que sustituyendo nos da un valor:

����������� c) Viga simplemente apoyada con carga triangular

����������� Supondremos variable la carga por unidad de longitud, aumentando linealmente desde 0 en el apoyo A hasta el valor p_m�x en el B

����������� Las cargas p dx sobre cada elemento diferencial de viga constituyen un sistema de vectores paralelos cuya resultante, la carga total , P, es:

y tiene por l�nea de acci�n la recta x=2/3 l. (La carga total P est� aplicada en el centro de gravedad del tri�ngulo).

����������� De las ecuaciones de la est�tica obtenemos las reacciones

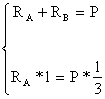
de donde obtenemos R_A y R_B:

����������� La ley de esfuerzos cortantes ser� �nica para cualquier secci�n de la viga

����������� La ecuaci�n de momentos ser� �nica y tendr� validez en 0 � x � l

����������� Para obtener el momento m�ximo, derivamos e igualamos a cero:

con lo que el momento m�ximo valdr�:

6. Torsi�n

6.1 Elementos que se encuentran sometidos a torsi�n

Los elementos de maquinas, ejes, �rboles que est�n efectuando transmisi�n de potencia de un motor o de una m�quina motriz a la unidad impulsada

Los elementos estructurales, cuando las fuerzas exteriores que recibe la viga o el voladizo, act�an en un plano que .no pasa por el eje de flexi�n de la misma.

����������� Generalmente estos momentos torsores son consecuencia de los momentos exteriores que se le transmiten al �rbol, (en el caso de elementos de m�quinas) normalmente en los lugares donde se colocan las poleas, ruedas dentadas, etc.

NOTA: Diferencia entre �rbol y eje:

����������� Los ejes se utilizan como medio para sostener un determinado elemento de m�quina, permiti�ndole que gire alrededor suyo

����������� Los �rboles de transmisi�n est�n destinados a transmitir momentos de rotaci�n a distancia

Para la representaci�n de momentos torsores emplearemos indistintamente flechas curvas, que indican el sentido de giro, una l�nea perpendicular al eje de la barra con dos c�rculos en representaciones planas. En uno de ellos se coloca un punto que indica la salida de la flecha curva hacia el lector, y en el otro un aspa que significa que la flecha entra en el plano alej�ndose del lector.

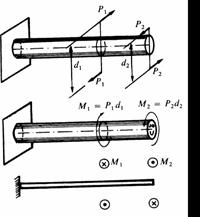
����������� El convenio de signos que adoptaremos para el momento torsor es el indicado. Se ha representando una rebanada del prisma mec�nico, es decir, la porci�n de barra comprendida entre dos secciones indefinidamente pr�ximas.

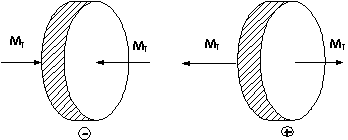
6.2 La TORSI�N en �rboles de secci�n circular. C�lculo de la tensi�n cortante m�xima de torsi�n.

En la teor�a elemental de la torsi�n se admite que en una pieza mec�nica sometida a torsi�n pura las secciones permanecen planas y la deformaci�n se reduce a una rotaci�n de las diferentes secciones alrededor de un eje� perpendicular a dichas secciones. Consigui�ndose buenos resultados en el estudio de piezas cuya secci�n recta sea un c�rculo o una corona circular (�rboles macizos o huecos).

����������� Si consideramos el esquema de la figura, la deformaci�n m�xima se produce en la base derecha de la pieza considerada y viene definida por el �ngulo de giro g, denominado �ngulo de torsi�n, que es el �ngulo de giro total de los extremos de la barra cil�ndrica.

����������� Esa deformaci�n consistir�a en un desplazamiento relativo entre cada dos secciones pr�ximas entre s�, sometidas a tensiones de cortadura, cuyas direcciones est�n contenidas en el plano determinado por las secciones rectas de la pieza.

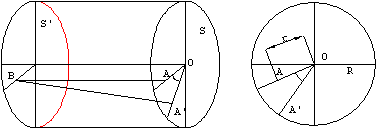
����������� El punto A de la secci�n pasar�a , despu�s de la deformaci�n, a la posici�n indicada como A�, y relacionando el arco, el �ngulo y el radio, podemos obtener la siguiente expresi�n

siendo g el �ngulo de deformaci�n por cortante, y por tanto la tensi�n de cortadura se puede expresar como:

y como r es la posici�n, respecto del centro de la secci�n circular, del punto considerado para estudiar la deformaci�n, la tensi�n cortante ser� entonces m�xima cuando r alcance su m�ximo valor, es decir R el radio de la secci�n.

����������� Por otra parte, el momento torsor, que es quien provoca la deformaci�n total de la pieza ser� entonces el momento total debido a las fuerzas cortantes en toda la secci�n.

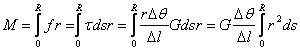
es decir, que el �ngulo de torsi�n es proporcional al momento torsor:

M= k q

Donde k es una constante de proporcionalidad que depende de las dimensiones de la pieza y del m�dulo de rigidez, G, del material:

Se puede establecer una relaci�n entre el momento torsor y la tensi�n m�xima de cortadura.

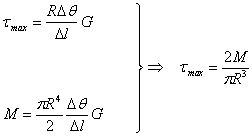
y como el momento de inercia polar de la secci�n circular es tendremos:

a la expresi�n I₀/R se le suele llamar m�dulo resistente a la torsi�n de la secci�n y se representa por W (L³)

����������� De la misma manera podemos obtener una expresi�n para el �ngulo de torsi�n q:

Tema 43:

ESFUERZOS MECANICOS. COMPOSICI�N Y REPRESENTACI�N DE ESFUERZOS. CALCULO DE ESFUERZOS EN PIEZAS SIMPLES

1. Introducci�n� a la Resistencia de Materiales

1.1. Concepto de S�lido R�gido

1.2. Hip�tesis de la Resistencia de Materiales

1.3. S�lido r�gido. Fuerzas exteriores e interiores

1.4. Condiciones generales de equilibrio de un s�lido r�gido

1.5. Cargas. Fuerzas externas

1.6. Reacciones y tipos de apoyos

2. Estudio de los estados solicitantes de un prisma mec�nico

3. Tracci�n y compresi�n

3.1. Esfuerzos y deformaciones

3.2. Resistencia a la tracci�n. Elasticidad y plasticidad

4. Cortadura

4.1. Esfuerzo normal y esfuerzo cortante en la tracci�n

4.2. Esfuerzo normal y esfuerzo cortante en la compresi�n

4.3. Teor�a elemental de la cortadura

4.4. Calculo de elementos a cortadura

5. Flexi�n

5.1. Hip�tesis del an�lisis de la flexi�n pura

5.2. Calculo del alargamiento unitario de una fibra cualquiera que diste �y� de la fibra neutra

5.3. Diagrama de s� para una secci�n. Ley de Navier

5.4. Criterio de signos para la ley de Navier

5.5. Flexi�n simple

5.6. Convenio de signos en flexi�n simple

5.7. Reacciones en los apoyos

5.8. Determinaci�n de los momentos flectores

6. Torsi�n

6.1. Elementos que se encuentran sometidos a torsi�n

6.2. La torsi�n en �rboles de secci�n circular. Calculo de la m�xima tensi�n cortante de torsi�n